This work has been published in IEEE Transactions on Neural Networks and Learning Systems.
Training compact networks typically fail due to what is known as the flat spot problem. This is where a gradient-descent algorithm converges on a local optima due to diminishing gradients that disable the learning process. Consider a neuron described by the activation function below:
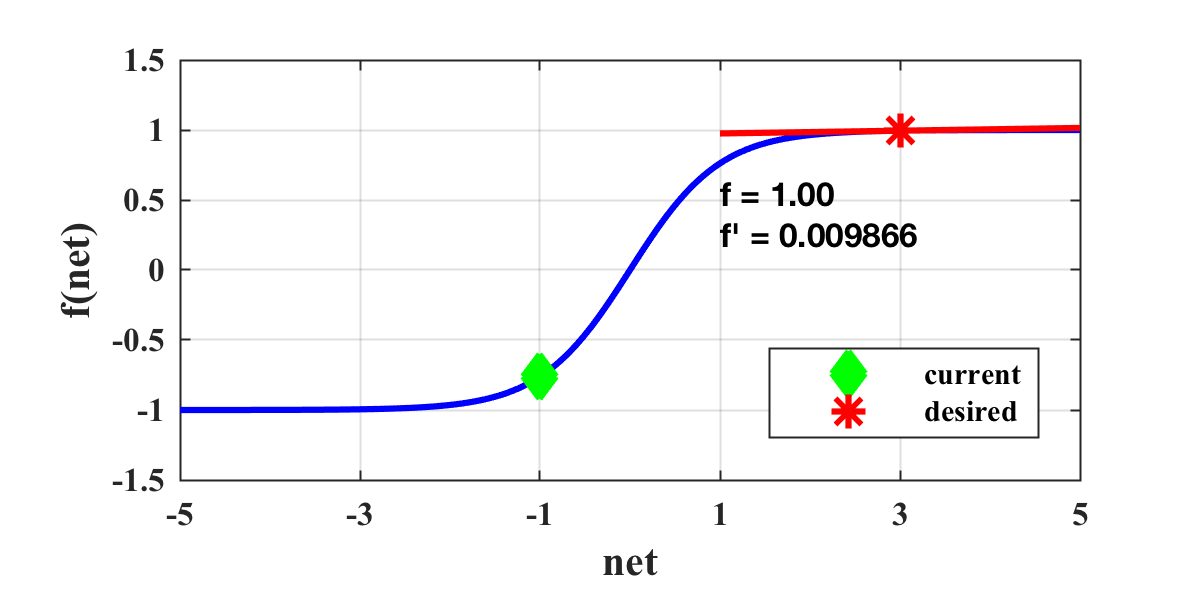
The weight update process is a function of the derivative; therefore, when the derivative approaches zero, the weight change will also approach zero. When this situation occurs, we would like to push the neuron activation back into the non-saturated region, such as:
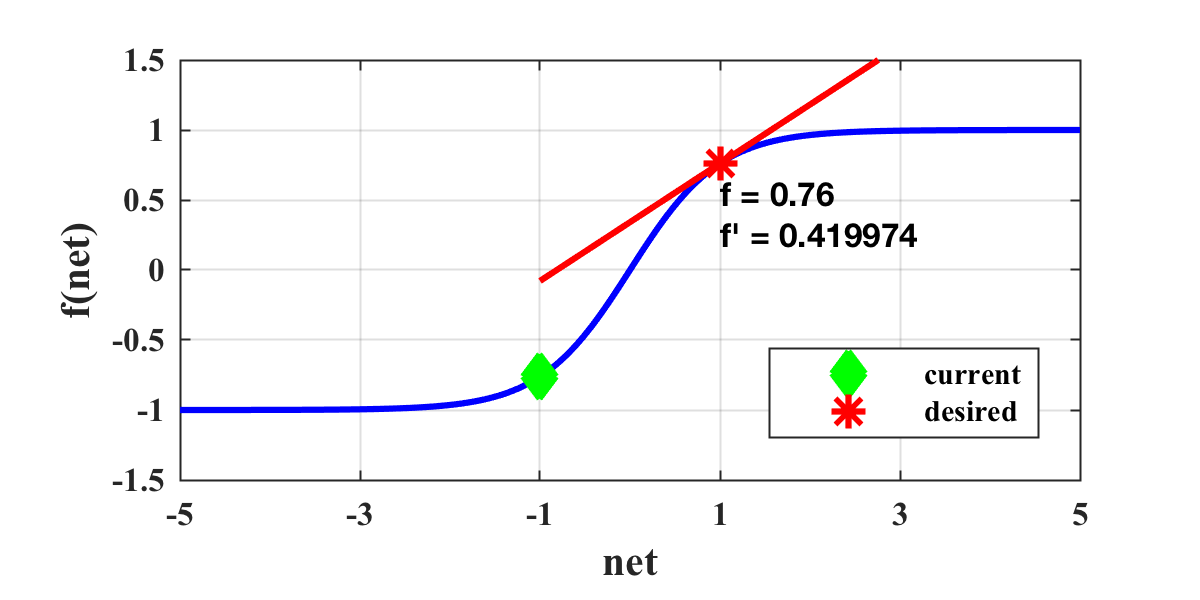
This project demonstrates that it is more effective to push these saturated neurons into more linear regions rather than restarting with new random weights. The methodology for doing this describes the scope of this project. What is the most computationally efficient way to return neuron activation into the liner region when local optima are met? How do we determine when a local optima has occurred? Do we target individual neurons or the entire network? This algorithm explores a new systematic approach that can be applied to several different gradient-descent algorithms and is proven to find successful solutions more often than competing approaches.
My code for this project can be found at https://github.com/jamessealesmith/nn_trainer_wc